T1
JOI 公司是一家以“没啥用发明”而闻名的公司。最近,JOI 公司开发了一款名为“没啥用编辑器”的编辑器。
在这个编辑器中,可以执行如下几种操作来输入某个字符串,设 $X$ 为屏幕上的字符串,$Y$ 为剪切板中的字符串,初始均为空串:
- 操作 A:输入字符 $c$,即将 $X$ 更新为 $X+c$。
- 操作 B:选择所有字符并剪切,即将 $Y$ 更新为 $X$,并将 $X$ 置为空串。
- 操作 C:将剪切板中的字符串粘贴到当前字符串末尾,即将 $X$ 更新为 $X+Y$。
对于字符串或字符 $x,y$,$x+y$ 表示将 $x$ 和 $y$ 顺次拼接得到的结果。使用一次操作 A,B,C 分别要花费 $A,B,C$ 单位时间。
你安装了“没啥用编辑器”,并想要尽可能快地输入一个长度为 $N$ 的字符串 $S$。
你需要计算出最少需要花费多少时间。
【数据范围】
对于所有数据,满足:
- $1\leq N\leq 2500$
- $S$ 是一个长度为 $N$ 的小写字母串。
- $1\leq A,B,C\leq 10^9$
3s, 2GiB
P9523 题解
区间 dp。$dp_{i,j}$ 表示凑出区间 $[i, j]$ 的最小代价。考虑枚举当前区间 $[i, j]$ 与 $k$,找到一个最大的 $p$,使得 $[i, j]$ 在区间 $[p, j]$ 中不重叠地出现了 $k$ 次。则有转移:
$$dp_{p,j} \leftarrow \min(dp_{p,j}, dp_{i,j} + B + k \times C + (j - p + 1 - k \times len) \times A)$$
以及最基本的:
$$dp_{i,j} \leftarrow \min(dp_{i+1,j} + A, dp_{i,j-1} + A, dp_{i,j})$$
这部分复杂度为 $O(\sum \frac{n}{j-i+1}) = O(n^2 \ln n)$。
现在就要考虑怎么找这个 $k$ 对应的 $p$。考虑 dp 求出 $S$ 每两个后缀的 $\mathrm{lcp}$,然后处理出对于一对 $(i, k)$ 的最大的 $j < i$,使得 $\mathrm{lcp}(S[i: n], S[j: n]) \geq k$。这个东西可以先记录 $= k$ 的情况,然后求后缀最大值。
时间复杂度 $O(n^2)$。
T2
D-taro 会给 Anna 一个整数,目标就是让 Anna 将这个整数发送给 Bruno。
游戏开始时,Anna 声明了一个在 $1$ 到 $2000$ 之间的整数 $m$,接下来他们玩 $Q$ 轮游戏。第 $i$ 轮游戏的过程如下:
-
D-taro 向 Anna 给出一个整数 $A_i$。
-
Anna 向通信设备输入两个数组 $s_i,t_i$,数组的每个元素 $s_i,t_i$ 应当是 $0$ 或 $1$,并且两者的长度相同且均为某个 $1$ 到 $m$ 之间的整数。
-
令 $u_i$ 为 $s_i$ 和 $t_i$ 经过乱序归并得到的结果,通信设备会向 Bruno 发送 $u_i$。
-
Bruno 告诉 D-taro 一个整数,如果这个整数和 $A_i$ 相同,Anna 和 Bruno 在这轮获胜。
以下是乱序归并的定义:
我们称数组 $Z$ 是数组 $X$ 和数组 $Y$ 经过乱序归并得到的结果当且仅当:存在一种划分方式,将 $Z$ 中的元素划成两个集合,满足:
- 第一个集合中的元素按在 $Z$ 中的位置顺次连接得到的数组是 $X$。
- 第二个集合中的元素按在 $Z$ 中的位置顺次连接得到的数组是 $Y$。
例如:数组 $[\underline{1},\underline{1},1,0,0,\underline{0}]$ 可以由数组 $[1,1,0]$ 和数组 $[1,0,0]$ 乱序归并得到。
请你实现 Anna 和 Bruno 的策略。
数据范围与评分方式
- $1\leq Q\leq 1000$
- $1\leq A_i\leq 10^{18}$
Subtasks
- $\text{(5 points) } A_i\leq 2000$
- $\text{(5 points) } A_i\leq 4\times 10^6$
- $\text{(3 points) } A_i\leq 10^7$
- $\text{(12 points) } A_i\leq 10^8$
- $\text{(15 points) } A_i\leq 10^{11}$
- $\text{(60 points)}$ 无特殊限制,评分方式如下:
这个子任务的得分是所有测试点得分的最小值。
对于某个测试点,他的得分由 $m$ 决定,如下表:
| $m$ | 得分 |
|---|---|
| $201\leq m\leq 2000$ | $40-25\times \log_{10}\left(\frac{m}{200}\right)$ |
| $161\leq m\leq 200$ | $40$ |
| $156\leq m\leq 160$ | $44$ |
| $151\leq m\leq 155$ | $48$ |
| $146\leq m\leq 150$ | $52$ |
| $141\leq m\leq 145$ | $56$ |
| $m\leq 140$ | $60$ |
AT_joisc2022_g 题解
将 $0/1$ 理解为 $\pm 1$,做一个前缀和。
构造 $\{t_{i}\}=10101\cdots$。
此时,将两者"乱序归并"后,其对 $\{s_{i}\}$ 前缀和的影响不大。
记 $a_{i}$ 为 $A$ 二进制下第 $i$ 位,$\forall i\in [1,60]$ 依次在 $\{s_{i}\}$ 末尾加入 $2+[a_{i}\ne a_{i-1}]$ 个 $a_{i}$(定义 $a_{0}=1$)
乱序合并后,维护 $s$ 表示 $\{u_{i}\}$ 的前缀和,每当 $|s|\ge 2$ 则得到下一位(根据 $s$ 的符号)并清空 $s=0$,这样就能忽略乱序归并 $\{t_i\}$ 带来的对前缀和的影响了。
事实上,上述做法本质上即能够确定满足每一个极长 $0/1$ 段的长度为 $\ge 3$ 的奇数的 $\{s_{i}\}$(第一段不一定是奇数,因为 $a_0=1$)
考虑进行映射,给每个符合条件的 $\{s_i\}$ 一个编号。
那么 Anna 仅需将需要存储的数作为编号找到对应的 $\{s_i\}$,然后传给 Bruno,Bruno 再反向查回编号即可得到答案。
注意到 Bruno 无法确定 $\{s_i\}$ 的长度,不妨在 $\{s_i\}$ 末尾插入一部分以 $01$ 为循环节的串。
最后还有一个优化:在 $\{s_{i}\}$ 开头增加一个 $A$ 的二进制最后一位,并在 $A$ 的最后一位和 $\{t_{i}\}$ 的第一位($1$)不同的前提下将所有 $\{s_{i}\}$ 和 $\{t_{i}\}$ 中的 $01$ 翻转,此时,$A$ 中的最后一位可以仅用 $1$ 个 bit 确定(此时 $u_0$ 必定等于 $A$ 的二进制最后一位),因此可以少用一个 $0/1$ 连续段。
DP 计数得上述形式且长度 $\le 140$ 的 $\{s_{i}\}$ 个数 $\ge 10^{18}$,可以通过本题。
T3
JOI 君是一位专业的团子师傅。在 JOI 君的店里,团子的颜色很有讲究。一共有 $N$ 种颜色,编号为 $1,2,\dots,N$。
一流团子串是 JOI 君的店里的招牌食品。制作一个一流团子串,需要将 $N$ 个颜色不同的团子串在一根竹签上。
对于每一种颜色,JOI 君都制作了 $M$ 个这种颜色的团子。因此,JOI 君总共有了 $NM$ 个团子。这些团子被编号为 $1,2,\dots,NM$。使用这些团子和 $M$ 根竹签,JOI 君希望串出 $M$ 个一流团子串。
为了避免在颜色上犯错误,JOI 君将会启用他的团子检测器。如果 JOI 君输入一些团子的编号,团子检测器会返回使用这些团子能制作的一流团子串的个数的最大值。当然,前提是充分使用竹签。
JOI 君希望能通过使用若干次团子检测器将 $NM$ 个团子分为 $M$ 组。其中,每一组包含 $N$ 个团子,且每种颜色的团子恰有一个。
JOI 君想在使用不超过 $50,000$ 次团子检测器的前提下完成这件事。
请写一个程序,对于给定的团子的信息,实现 JOI 君使用不超过 $50,000$ 次团子检测器来完成任务的策略。
【数据范围】
对于所有测试数据,满足:
- $1 \le C_i \le N$ $(1 \le i \le NM)$。
- 对于每个 $j$ $(1 \le j \le N)$,恰有 $M$ 个 $i$ $(1 \le i \le NM)$ 满足 $C_i = j$。
- $N,M$ 是正整数。
- $C_i$ $(1 \le i \le NM)$ 是一个 $[1,N]$ 内的整数。
P9529 题解
我们可以把每个串看成一个集合,所以总共有 $m$ 个集合,对于每个团子,我们尝试将其插入某个集合中。插入时需要维护以下性质:
一:每个集合内的每个团子的颜色互不相同。
二:同一种颜色的团子是按串串的编号从左到右放到每个串串中的。
所以现在问题变为了如何检验这个颜色的团子放在哪里。
而我们似乎只能用 Query(x[]) 函数来检验,但是我们总共只能调用 $50000$ 次 Query(x[]) 函数。而团子的总数最多有 $m \times n$ 即 $10000$ 个。所以我们需要在最多调用 $5$ 次 Query(x[]) 函数的情况下来求出这个团子放在哪。
我们根据这些想到可以二分,因为根据性质二,这种颜色的团子一定是前面一段串串有,后面的串串全部都没有的,所以可以通过二分的方式来查找。而二分要调用大约 $\log_2 25$ 次 Query(x[]) 函数,而 $4 \leq \log_2 25 \leq 5$,刚好小于等于 $5$,所以我们接下来就要考虑怎么二分了。
我们先假设前几个串串上已经有了一些团子,就像这样:
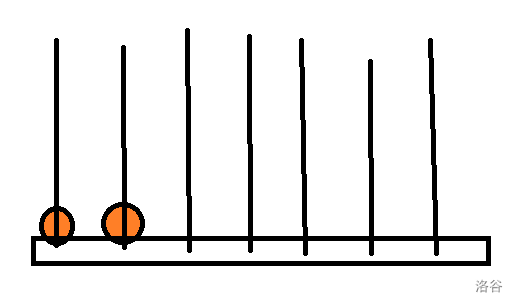
那么对于下一个这种颜色的团子,如果我们放在这两个已经有这种颜色的串上,就像这样:
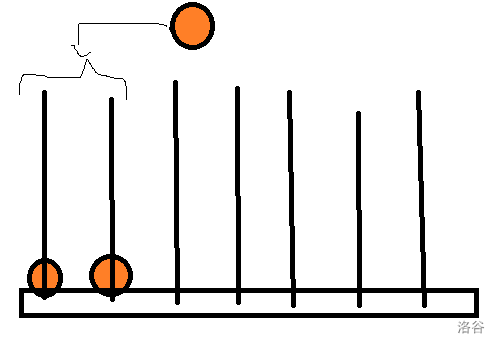
由于这种颜色的团子的个数等于总的串串数,所以如果我们放在这两个已经有这种颜色的串上的话,所有剩下的团子就没有办法组成剩下串串的个数个一流团子串。(建议自己在纸上画一下)欸,这不就可以用到 Query(x[]) 函数了吗!
我们设当前的团子放在第 $mid$ 个串上,那么如果所有没有处理的团子和第 $mid + 1$ 到第 $m$ 个串上的所有团子加起来能做出至少 $m - mid$ 个一流团子串的话,这个团子就可以放在第 $mid$ 个串上。就像这样(能放的情况):
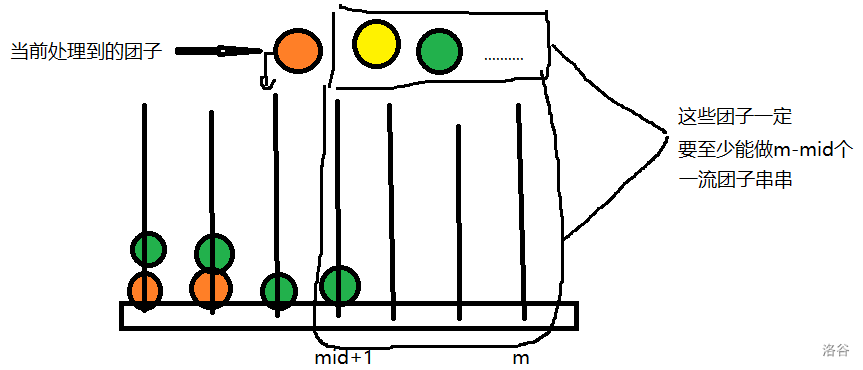
我们钦定第 $i$ 个团子可以放在第 $j$ 个串上,那么它一定能放在第 $k\in[1,j]$ 个串上。同时,如果我们现在放到了 $j$ 上,那么对于第 $[i+1,nm]$ 个的团子,这种放到 $j$ 上的方案必定不劣于放到 $k$ 上,因为这样 $[mid + 1, m]$ 一定能做出更多团子。
我们就用这个进行二分,如果能做出至少 $m - mid$ 个一流团子串,我们就把 $r$ 赋值为 $mid - 1$,同时用 $ans$ 记录下 $mid$,否则就把 $l$ 赋值为 $mid + 1$,二分的边界条件为 $l \leq r$。二分完后就把这个团子放入第 $ans$ 个串串中。把每个团子都这样处理后这道题就做完了。
评论
0 条讨论
暂时还没有评论,欢迎留下第一条反馈。