补全证明：棋盘格子配对问题

一、从格子配对到二分图最大匹配

1. 图模型

当前棋盘是 $n \times n$ 的，每个格子要么黑要么白。我们要选出若干对格子 $((x_1,y_1),(x_2,y_2))$，满足：

1. $(x_1,y_1)$ 是白，$(x_2,y_2)$ 是黑；
2. 在同一行或同一列；
3. 每个格子最多被用一次。

用图论语言建模：

• 把所有白格子作为二分图左部的点；
• 把所有黑格子作为二分图右部的点；
• 如果一个白格子和一个黑格子在同一行或同一列，就在它们之间连一条边。

那么：

• 一条边对应一个合法的格子对（白 → 黑）。
• 一组互不相交的边（没有公共端点）对应一组互不相交的格子对。

因此： 要选的格子对数量 = 这个二分图的最大匹配大小。

这就证明了“答案即为二分图最大匹配”的那一步。

二、从最大匹配到最大独立集

一个小知识：在任意图中，有如下关系： $$ \text{最大独立集大小} + \text{最小点覆盖大小} = |V| $$ 其中 $|V|$ 为点数。

在二分图中还有著名的 Kőnig 定理：

在任何二分图中： 最大匹配大小 = 最小点覆盖大小。

于是对我们这个二分图： $$ \text{最大匹配} = \text{最小点覆盖} = |V| - \text{最大独立集} $$

本题中点就是所有格子，数量为 $n^2$。于是： $$ \text{答案} = \text{最大匹配大小} = n^2 - \text{最大独立集大小} $$

所以求最大匹配 ⇔ 求最大独立集，求后者更方便做结构分析。

三、最大独立集在棋盘上的结构

回忆一下图的定义：

• 点：每个格子（带颜色）；
• 边：同一行或同一列中，颜色不同的一对格子。

独立集：点集 $I$，其中任意两点之间没有边。 也就是：不会出现同一行 / 列中同时选了一个黑格子和一个白格子。

1. 每行每列只能选一种颜色 —— 证明

结论： 在任意一个独立集中，对每一行 / 每一列：

如果这一行（列）里被选的格子不是空的，那么它们的颜色都相同。

证明：

• 反设某一行 $x$ 中，在独立集里同时选了一个黑格子 $(x,y_1)$ 和一个白格子 $(x,y_2)$。
• 按图的定义：只要「同一行且颜色不同」就有一条边。
• 所以 $(x,y_1)$ 与 $(x,y_2)$ 之间有边。
• 但独立集中任意两点之间不能有边，矛盾。

同理，对列也是一样。

所以： 最大独立集在原方阵中的形态：每一行 / 每一列中选的格子只会有一种颜色。

这就补上了题解里那句 “形态” 的严谨理由。

四、用集合 $S,T$ 描述独立集

根据上面的结构，我们可以这样编码一个独立集：

• 对每一行，决定：这行“如果选格子的话”，是选黑还是选白；
• 对每一列，也做同样的决定。

我们用两个集合来表示“选白”的行列：

• 集合 $T$：表示选择白色的行；
• 集合 $S$：表示选择白色的列。

于是：

• 行 $x \in T$：这一行里若有选中的格子，则只能选 白格子；
• 行 $x \notin T$：这一行里若有选中的格子，则只能选 黑格子；
• 列 $y \in S$：这一列里若有选中的格子，则只能选 白格子；
• 列 $y \notin S$：这一列里若有选中的格子，则只能选 黑格子。

把行和列的选择合在一起，一个格子 $(x,y)$ 能被选，当且仅当：

• 若它是白色：行、列都选择白：$x \in T, y \in S$；
• 若它是黑色：行、列都选择黑：$x \notin T, y \notin S$。

我们把这两类格子全部选上，就能得到一个独立集，而且显然是在固定 $(S,T)$ 下数量最多的独立集（因为所有合法格子都选了）。

所以对每一组 $(S,T)$，最大独立集大小就是：

• 白格子且 $x\in T, y\in S$ 的个数
• 加上黑格子且 $x\notin T, y\notin S$ 的个数。

题解中对应那句：

对于点 $(x, y)$：

• 若目前为白且 $x \in T, y \in S$，贡献 $1$；
• 若目前为黑且 $x \notin T, y \notin S$，贡献 $1$。

至此，“枚举 $S,T$” 这一段就完全合理了。

五、关键观察：行贡献只和 $|S|$ 有关

题解接下来做了一个非常关键的“降维观察”：

1. 先只枚举列的选择，把“哪些列选白”设为集合 $S$；
2. 初始先假定“所有行都选白”（即 $T = \{1,\dots,n\}$）；
3. 然后再考虑某些行从“选白”变成“选黑”的收益。

1. 基础方案：所有行选白

设：

• 每列 $j$ 的白格子数为 $a_j$。

当所有行都选白（$T=\{1,\dots,n\}$）时：

• 对于列 $j\in S$：行、列都选白，所以所有的白格子都可以被选；
• 对于列 $j\notin S$：列选黑，这里没有格子同时满足“行、列都白”。

于是此时独立集的大小是： $$ \text{Base}(S) = \sum_{j \in S} a_j $$

这就是题解里的那句：

设集合 $S$ 中的列选了白，所有行都选了白。贡献为 $S$ 列中白格子个数。

2. 把某一行从“白行”改为“黑行”的增量贡献

重点：我们在固定 $S$ 的前提下，看某一行改色对答案的影响。

设这一行是第 $i$ 行：

• 这一行的黑格子数为 $b_i$；
• 这一行总共 $n$ 个格子。

我们考虑这一行由“选白”（在 $T$ 中）变为“选黑”（不在 $T$ 中）时，独立集大小变化多少。

把这一行里的格子拆成 4 种情况（按颜色 + 所在列是否在 $S$）：

1. 情况 1：白格子，并且所在列在 $S$。

   • 在“行白、列白”时： 行、列都选白 → 这个白格子被选中。
   • 在“行黑、列白”时： 行选黑、列选白 → 白格子不再能被选中。

   这类格子：每个**-1**。

2. 情况 2：白格子，并且所在列不在 $S$。

   • “行白、列黑”：此时这个白格子不能被选（列选黑）；
   • “行黑、列黑”：行也黑了，还是不能选白格子。

   → 这类格子对答案无影响，贡献 0。

3. 情况 3：黑格子，并且所在列在 $S$。

   • “行白、列白”：显然不能选黑格子；
   • “行黑、列白”：依然不能选黑格子（列不是黑）。

   → 这类格子贡献 0。

4. 情况 4：黑格子，并且所在列不在 $S$。

   • “行白、列黑”：行选白，这个黑格子不能选；
   • “行黑、列黑”：行、列都选黑，这个黑格子可以选！

   → 每个贡献 +1。

把这四种情况放在一起：

• 本来被选的：只有情况 1；
• 修改后被选的：只有情况 4；

所以这一行净变化 = $$ \text{（情况 4 的个数）} - \text{（情况 1 的个数）} $$

设：

• 这一行在列 $S$ 中的黑格子数为 $B_S$；
• 在列 $S$ 中的白格子数为 $W_S$；

则：

• “情况 1 的个数” = $W_S$；
• “情况 4 的个数” = 这一行不在 $S$ 中的黑格子数 = 总黑格子数 $b_i$ 减去在 $S$ 中的黑格子数 $B_S$： $$ \text{情况 4 个数} = b_i - B_S $$

于是净贡献： $$ \Delta_i = (b_i - B_S) - W_S = b_i - (B_S + W_S) $$

注意到：

• 一行里在列 $S$ 中一共有 $|S|$ 个格子；
• 它们要么是黑要么是白，所以 $B_S + W_S = |S|$。

于是： $$ \boxed{\Delta_i = b_i - |S|} $$

这个式子里已经没有 “$S$ 中哪些具体列” 的信息了，只剩下 $|S|$！

这正是题解中那句 “惊人结论” 的严密证明：

一行从白变黑对答案的贡献是： 行内黑格子数 $b_i$ 减去白列数 $|S|$。 因此贡献和 $S$ 的具体内容无关，只和 $|S|$ 有关。

3. 对整张棋盘的贡献

在固定列集合 $S$ 的前提下：

• 基础方案（所有行选白）贡献：$\sum_{j\in S} a_j$；
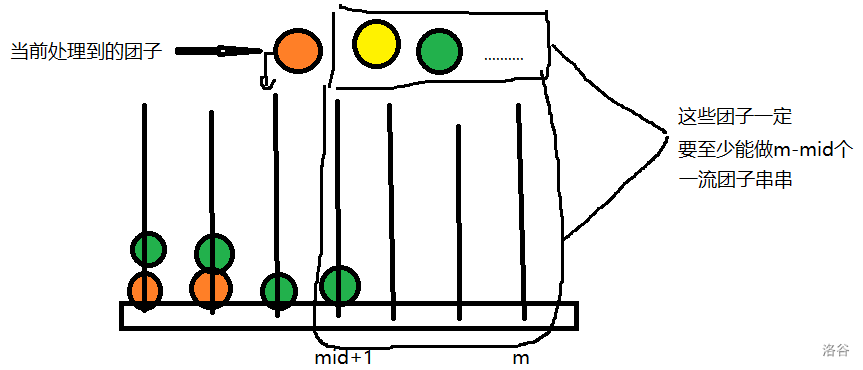
• 对于每一行 $i$，如果把它从白改黑有正收益 $\Delta_i = b_i-|S|>0$，我们就把这一行改成黑行；否则就保持白行不动。

于是整张图在给定 $S$ 时的最大独立集大小为： $$ \text{MIS}(S) = \sum_{j\in S} a_j + \sum_{i=1}^{n} \max(0, b_i - |S|) $$

设 $|S| = x$，可以写成： $$ \text{MIS}(S) = \sum_{j\in S} a_j + \sum_{i=1}^{n} \max(0, b_i - x) $$

对于固定的 $x$（即固定的 $|S|$），第二项只跟 $x$ 有关，与具体的 $S$ 无关； 第一项要让 $\sum_{j\in S} a_j$ 最大，只要选出“白格子数最多的 $x$ 列”。

六、排序列得到最终公式

记：

• 对所有列的白格子数 $a_1,\dots,a_n$ 按降序排序，得到 $A_1 \ge A_2 \ge \dots \ge A_n$。

对于给定的 $x = |S|$，最优的列集合是取白格子最多的前 $x$ 列，因此 $$ \max_{|S| = x} \sum_{j\in S} a_j = \sum_{i=1}^{x} A_i $$

于是最大独立集大小可以写成： $$ \text{MIS} = \max_{0 \le x \le n} \left\{ \sum_{i=1}^{n} \max(0, b_i - x) + \sum_{i=1}^{x} A_i \right\} $$

题解里的公式就是这个： $$ \max_{x=0}^n \left\{ \sum_{i=1}^n \max(0, b_i - x) + \sum_{i=1}^x A_i \right\} $$

最后答案（最大匹配）为： $$ \text{Ans} = n^2 - \text{MIS} = n^2 - \max_{0\le x\le n} \left\{ \sum_{i=1}^{n} \max(0, b_i - x) + \sum_{i=1}^{x} A_i \right\} $$

这一步就把“图论 + 结构分析”完整闭环起来了。

七、数据结构那块再解释一下（和代码对应）

题解里后面的“数据结构优化”+ 代码，其核心就是如何维护上面的函数： $$ F(x) = \sum_{i=1}^{n} \max(0, b_i - x) + \sum_{i=1}^{x} A_i $$

并支持单点修改 $a$ / $b$ 后快速更新所有 $x$ 的 $F(x)$ 值的最大值。

1. 静态建初值（对应代码里的 build 部分）

• 首先用「二维差分 + 一维线段树扫描」做所有矩形翻转，得到初始颜色。

• 在这个基础上：

  • $a$：每一“列”的白格子数（代码里行列交换了）；
  • $b$：每一“行”的黑格子数。

• 把 $a$ 排序得到 $A$，构造与 $A$ 有关的那一段 $\sum_{i=1}^x A_i$；

• 利用差分数组 tb 把 $\sum_{i=1}^n \max(0, b_i - x)$ 写成一系列对区间 $[0,n]$ 上的加法，最后得到 tt 线段树叶子上存的就是 $F(x)$ 的值；

• 取 tt.qrymx() 就得到 $\max_x F(x)$。

上面这些，在前面我们已经从数学上验证过 tb + 区间加的正确性，这里就不重复展开。

2. 修改一个格子时的更新（对应后半段代码）

每次单点翻转 $(r,c)$ 的颜色，会导致：

• 所在行 / 列某一维度的“白格子数” +1 或 -1；
• 所在列 / 行另一维度的“黑格子数” +1 或 -1。

在公式里，就是某个 $a_r$ 变为 $a_r \pm 1$，某个 $b_c$ 变为 $b_c \pm 1$。

而：

• 改 $a_r$：影响排序后的 $A$ 数组中某个元素所在位置的值， 再通过线段树对 一段前缀 / 后缀做区间加减（因为 $\sum_{i=1}^{x} A_i$ 对所有 $x$ 有规律的影响）； 代码里用 al[]、ar[] 来维护某个“值大小段”在排序后的位置区间。
• 改 $b_c$：直接在 $F(x)$ 中对所有 $x \le b_c$ 或 $x \le b_c-1$ 做线性变化，也可以被翻译成区间加， 于是同样用线段树实现。

这就是代码中 tt.add(区间, v) 的逻辑来源： 本质就是把对 $a,b$ 的单点变化，转化成对所有 $x$ 上 $F(x)$ 的一段“斜率+截距”变化。

每次改完后，再取一次 tt.qrymx() 就是新的 $\max_x F(x)$，再用 $n^2 - \text{这个值}$ 输出答案。

到这里，题解里的几个“跳得比较快”的点：

1. 最大匹配 → 最大独立集；
2. 最大独立集的“行列同色”结构；
3. 用 $S,T$ 来描述独立集；
4. 一行从白改黑的增量是 $b_i - |S|$ 且与 $S$ 的具体内容无关；
5. 排序列得到 $\max_x {\sum \max(0,b_i-x) + \sum_{i\le x} A_i}$；

都已经补上完整的证明和推导了。

性质 B：给定树 $T$，其最大独立集（MIS）是唯一的，记为 $I$。
我们要算：随机算法返回的计数 $c$ 恰好等于 $|I|$ 的概率。

算法是：

1. 所有点白色，$c=0$；
2. 反复：从所有白点中等概率选一个 $u$，把 $u$ 和所有仍为白色的邻居染黑，c++；
3. 无白点时停，返回 $c$。

（注意：最后选出来的是某个极大独立集的大小，不保证最大。）

经典套路：
这类“每次在剩余元素里随机选一个做决策”的过程，可以等价为：

先给所有点一个独立的随机实数权值（优先级）$w_v \sim U(0,1)$，
按权值从小到大依次扫：如果当前点没有已选邻居，就把它选入集合。

所以我们只需要研究：

对随机权值 $w$，贪心算法得到的独立集等于唯一 MIS $I$ 的概率。

记 $O = V \setminus I$（不在 MIS 里的点）。

首先两件显然的事：

1. 因为 $I$ 是最大独立集，所以它也是极大独立集：
   $\forall u\in O$，都有邻居在 $I$。否则可以把 $u$ 加进去得到更大独立集。
   所以 $I$ 是支配集：每个 $O$ 点至少连着一个 $I$ 点。
2. $I$ 独立：任意两点 $v_1,v_2\in I$ 没有边。

我们想要：贪心选出的集合恰好为 $I$，即：

• 没有 $O$ 点被选入；
• 所有 $I$ 点都被选入（否则选不满 $|I|$ 就不可能是 MIS，且唯一性也会炸）。

考虑某个 $u\in O$。

要阻止 $u$ 被贪心选中，必须在它“轮到被考虑”之前，已经有某个邻居被选了来把它“染黑”。

但注意：被选中的点最终必须都在 $I$，否则结果就不是 $I$。

因此：对于一个合法的随机权值配置（即最终得到 $I$），每个 $u\in O$ 都必须满足：

• 在 $\{u\} \cup (N(u) \cap I)$ 中，最小权值的点属于 $I$，而不是 $u$。

否则，如果 $w_u$ 比所有邻居的 $I$-点都小，那在它被扫描时没有已选邻居，它就会被选进集合，矛盾。

进一步，还要排除“被别的 $O$ 点挡住”的情况：
如果最小的是某个 $O'$，那 $O'$ 本身会被选中（因为没人挡它），又矛盾。
所以在“成功的”权值配置下，每个 $O$ 点的“拦截者”必须是 $I$ 点。

于是得到充分必要条件（在唯一 MIS 条件下）：

贪心输出 $I$ 当且仅当
对所有 $u\in O$，有
$$ w_u > \min_{v \in N(u)\cap I} w_v. $$

换句话说，至少有一个连着它的 $I$-点比它更早出现，从而把它杀掉。

而一旦这条对所有 $u\in O$ 成立，由于：

• $I$ 自身独立，不会互相杀；
• 每个 $O$ 的杀手来自 $I$，没有 $O$ 被选入；
• $I$ 是极大独立集（支配所有点）；

贪心一定正好选出所有 $I$，不多不少。

这个条件只依赖「$I$ 与每个 $O$ 的邻接关系」和权值顺序，
不再直接看 $O$-$O$ 边——因为那些边一旦起作用就会导致 $O$ 被选，已经被我们排除了。

现在只关心：图上 $I$ 与 $O$ 之间的边。

构造图 $H$：

• 顶点仍是 $V$；
• 只保留所有 $I$-$O$ 边，删去 $I$-$I$（本来就没有）和 $O$-$O$ 边。

原图是树 ⇒ 去掉一些边后 $H$ 是一片森林。
每个连通块只在 $I$ 与 $O$ 之间交替。

而我们的成功条件是：

对每个 $u\in O$，$w_u > \min_{v\in N_H(u)} w_v$。

关键：每个 $u\in O$ 的邻接 $I$-点都在这片 forest 里，耦合关系只发生在同一个连通分量中。
不同连通分量的权值独立，条件也独立 ⇒
总概率 = 各连通分量成功概率的乘积。

所以我们只需求：

在一个连通的 $I$-$O$ 树上，这些不等式成立的概率。

我们对每个连通分量：

1. 随便选一个 $I$-点做根 $r$。
2. 把它看成根在 $I$ 侧的二叉/多叉树，层次 I-O-I-O…

对这个树做从叶到根的 DP。

• 对一个 $I$-点 $v$ 定义 $G_v(x)$：
  在「父亲那边给的约束已经满足」前提下，在 $w_v = x$ 时，它整棵子树中所有不等式成立的条件概率。
  （你可以理解为：从 $v$ 往下那块，只看局部约束后留下来的“合法权值配置密度”。）

• 对一个 $O$-点 $u$ 定义 $M_u(x)$：
  在「与它连着的父亲 $I$-点权值为 $x$」时，整棵以 $u$ 为根的子树满足所有约束的条件概率。

因为所有约束和分布都是多项式/积分可写的形式，这两个函数都将是关于 $x$ 的多项式（模意义下）。

I 点转移

若 $v$ 是 $I$ 点，它的子节点全是 $O$ 点 $u$：

• 条件是：所有这些 $u$ 的子树在给定 $w_v=x$ 下都合法；
• 子树独立 ⇒
  $$ G_v(x) = \prod_{u \text{是 }v\text{的子 }O} M_u(x). $$

O 点转移

设 $u$ 是 $O$ 点，有父 $I$-点权值 $x$，子 $I$-点为 $v_1,\dots,v_k$。

约束只有两个部分：

1. 对这个点本身：
   $$ w_u > \min(x, w_{v_1},\dots,w_{v_k}) $$
2. 每个子 $I$-点 $v_i$ 的子树约束，用 $G_{v_i}(w_{v_i})$ 表达。

权值独立均匀，我们要算：
$$ M_u(x) = \mathbb{P}\Big( w_u > \min(x,w_{v_1},\dots,w_{v_k}),
\bigwedge_i \text{子树 }i\text{合法} ,\Big|, w_{\text{parent}}=x \Big). $$

1. 对每个子 $v_i$，它的权值 $y_i$ 均匀于 $[0,1]$，子树合法概率为 $G_{v_i}(y_i)$。
2. 定义
   $$ T_i(t) = \int_t^1 G_{v_i}(s),ds, $$
   表示「在 $y_i \ge t$ 时子树合法的积分贡献」。

我们先计算在忽略 $u$ 的限制的前提下，合法方案出现的概率 $C$。

然后再减去再方案合法的前提下，不满足 $u$ 的限制的概率。

前者是显然的 $C = \prod_{i=1}^k T_i(0)$

后者我们需要 $\exists v\in I, w_u < w_v$ ①，保证 O 点 $u$ 先于 I 点 $v$ 被选。

但是我们发现，仅仅是存在并不正确，考虑 I-O-I 的情况下，我们把两个 I 分别称为 $v_1,v_2$，且 $w_{v_1} < w_{v_2}$。

如果 $w_{v_1}<w_u<w_{v_2}$，虽然 $u$ 的限制的确被满足了，但我们的方案就不合法了。因为 $v_1$ 被选后 ban 了 $u$，$u$ 无法被选，而我们期望 $v_1,u,v_2$ 均被选。

所以上面条件①的存在应当改成任意。

那么答案就是

$$ M_u(x) = C - \int_0^{x} \prod_{i=1}^k T_i(t),dt, $$

对该连通分量的根 $I$-点 $r$：

• 没有父亲约束，只需要对 $w_r$ 在 $[0,1]$ 上积分：
  $$ P_{\text{comp}} = \int_0^1 G_r(x),dx. $$

所有都是多项式，用模意义的积分（系数除以 $k+1$）即可。

$$ \begin{aligned} [f({\cal P})=f({\cal Q})]&=\sum_{\sf x}[P_{\sf x}=Q_{\sf x}] \\ &=\sum (P_{\sf x}\land Q_{\sf x})\lor(\overline{P_{\sf x}}\land \overline{Q_{\sf x}}) \\ &=\sum 1-\big(1-(P_{\sf x}\cdot Q_{\sf x})\big)\cdot\big(1-(1-P_{\sf x})\cdot (1-Q_{\sf x})\big) \\ &=\sum 2P_{\sf x}Q_{\sf x}-(P_{\sf x}+Q_{\sf x})+1 \\ &=\kern{-20px}\sum_{\substack{A\sube f({\cal P})\cap f({\cal Q})\\B\sube f({\cal P}),C\sube f({\cal Q})}}\kern{-18px}[A\cap B=\varnothing][A\cap C=\varnothing][B\cap C=\varnothing] 2^{|A|}(-1)^{|B|+|C|} \\ &=\kern{-19px}\sum_{S\sube f({\cal P}),T\sube f({\cal Q})}\kern{-17px}2^{|S\cap T|}(-1)^{|S|+|T|} \end{aligned} $$

Generated by GPT 5 Thinking

1. 记号与基本化简

对非负整数 $i,j$，定义 $$ f(i,j)=\min\{x\in\mathbb Z_{\ge 0}\mid i+0.5+x>(j\oplus x)\}. $$

引理 1（去掉 0.5）

对任意整数 $A,B$，有 $$ A+0.5>B\quad\Longleftrightarrow\quad A\ge B . $$ 因此 $$ f(i,j)=\min\{x\in\mathbb Z_{\ge 0}\mid i+x\ge (j\oplus x)\}. \tag{1} $$

证明. 右端是整数，左端是“整数+0.5”。若 $A\ge B$ 则 $A+0.5>B$；反之若 $A+0.5>B$，因为 $A,B\in\mathbb Z$，只可能是 $A\ge B$。∎

接下来用一个标准位运算恒等式：

引理 2（XOR–AND 恒等式）

对任意非负整数 $u,v$，有 $$ u\oplus v = u+v-2(u\&v). $$ 从而 $$ (j\oplus x)-x = j-2(j\&x). \tag{2} $$

证明. 众所周知 $(u\oplus v)+2(u\&v)=u+v$。移项即得。∎

将 (2) 代入 (1)，得到

$$ \begin{aligned} f(i,j) &=\min\{x\ge 0\mid i+x\ge j-2(j\&x)\} \\ &=\min\{x\ge 0\mid j-2(j\&x)\le i\}. \end{aligned} \tag{3} $$

令 $y=(j\&x)$。当 $x$ 枚举全部非负整数时，$y$ 恰好枚举 $j$ 的所有子掩码（即 $0\le y\le j$ 且 $(y\&\sim j)=0$）。并且对任何给定子掩码 $y$，取 $x:=y$ 就能达到同一个 $j\&x=y$ 且使 $x$ 最小。因此 (3) 等价于

$$ f(i,j)=\min \{y\subseteq j\mid j-2y\le i\}, \tag{4} $$ 其中“$y\subseteq j$”表示 $y$ 是 $j$ 的子掩码。

由 (4) 立刻得到两个基本性质：

• 若 $i\ge j$，则取 $y=0$ 合法，故 $f(i,j)=0$。
• 否则 $i<j$，令 $$ t:=\left\lceil\frac{j-i}{2}\right\rceil\in\{1,2,\dots,\left\lceil\frac j2\right\rceil\}, $$ 则 (4) 等价于“在 $j$ 的子掩码中找不小于 $t$ 的最小者”。

为此定义：

定义. 对整数 $j\ge 0$ 与 $t\in\mathbb Z$，定义 $$ s_j(t):=\min \{y\subseteq j\mid y\ge t\},\qquad\text{若集合为空则不定义。} $$ 为了统一边界，约定 $s_j(t)=0$ 当 $t\le 0$。

于是得到一个完全显式的表达式：

$$ f(i,j)=s_j\left(\left\lceil\frac{j-i}{2}\right\rceil\right).\tag{5} $$

特别地，(5) 也涵盖了 $i\ge j$ 的情形（此时 $t\le 0$，按约定 $s_j(t)=0$）。

2. 对 $g(j)$ 的配对化简

题目中的 $$ g(J):=\sum_{i=0}^{10^{10^{100}}} f(i,J) $$ 由于 $f(i,J)=0$（当 $i\ge J$），实际上是 $$ g(J)=\sum_{i=0}^{J-1} f(i,J)=\sum_{i=0}^{J-1} s_J\left(\left\lceil\frac{J-i}{2}\right\rceil\right). $$

将 $i$ 与 $J-1-i$ 成对，注意 $$ \left\lceil\frac{J-i}{2}\right\rceil= \begin{cases} t,&\text{某个 }t, \\ t,&\text{配对项也给出同一个 }t, \end{cases} $$ 于是每个 $t$（除了 $J$ 为奇数时的中位 $t=(J+1)/2$）均恰好出现两次。严格化写成：

$$ g(J)=2\sum_{t=1}^{\lfloor J/2\rfloor} s_J(t)+[J\text{ 为奇}]\cdot s_J\big((J+1)/2\big). \tag{6} $$

（这里 $[P]$ 为命题 $P$ 的指示函数。）

3. $s_j(\cdot)$ 的分段与 $S(j)$ 的递推

记 $j$ 的最高位为 $2^k$（即 $2^k\le j<2^{k+1}$），把 $$ j=2^k+r,\qquad 0\le r<2^k. $$ $j$ 的子掩码分为两类：

• 不含最高位：恰是 $r$ 的全部子掩码；
• 含最高位：形如 $2^k+u$，其中 $u$ 是 $r$ 的子掩码。

据此得到对任意 $t$ 的分段表达：

$$ s_j(t)= \begin{cases} s_r(t), & 1\le t\le r \\[2pt] 2^k, & r<t\le 2^k \\[2pt] 2^k+s_r(t-2^k), & 2^k<t\le 2^k+r. \end{cases}\tag{7} $$

注：题目的查询保证 $a_l=1$，于是 $\mathrm{val}(l,r)$ 的最高位固定存在，即对应用到的 $t$ 都不超过 $j$，所以 (7) 的定义域覆盖了我们需要的全部 $t$。

为了处理 (6) 中的 $\sum s_J(t)$，定义前缀和函数 $$ S(x):=\sum_{t=1}^{x}s_x(t),\qquad S(0):=0. \tag{8} $$

利用 (7) 对 $x=j=2^k+r$ 做拆分求和，直接计算可得

$$ \boxed{S(2^k+r)=2S(r)+4^k},\qquad S(0)=0. \tag{9} $$

这是一条核心递推：把一个数剥去最高位后，对“右侧剩余”的贡献加倍，同时加上最高位的平方 $4^k$。

4. $g(J)$ 的统一闭式（不分奇偶）

回到 (6)。注意当 $J=2^k+r$ 时， $$ \lfloor J/2\rfloor - r \in \{0,1,\dots,2^k-r\},\quad [J\text{ 为奇}]=J-2\lfloor J/2\rfloor. $$ 将 (7) 的前两段代入 (6)（因为 $r<\frac{J}{2}\le 2^k$ 恒成立；当 $r=\lfloor J/2\rfloor$ 时第二段恰为空和也成立），并整理奇偶项，得到

$$ \begin{aligned} g(J) &=2\Big(S(r)+\big(\lfloor J/2\rfloor-r\big)\cdot 2^k\Big)+[J\text{ 为奇}]\cdot 2^k \\ &=2S(r)+\big(2\lfloor J/2\rfloor+[J\text{ 为奇}]-2r\big)\cdot 2^k \\ &=2S(r)+\big(J-2r\big)\cdot 2^k =2S(r)+4^k-2^k r. \end{aligned}\tag{10} $$

上式自动统一了奇偶两种情形（利用恒等式 $2\lfloor J/2\rfloor+[J\text{ 为奇}]=J$）。这给出 $g(J)$ 的一个非常简短的表达：只需知道 $J$ 的最高位 $2^k$ 与其“尾部” $r$，以及 $S(r)$。

结合 (9)，我们可以递归地求出 $S(r)$（不断剥最高位，直到 0），于是 $g(J)$ 也就随之得到。这个过程的递归深度等于 $r$ 的二进制位数（$\le \lfloor\log_2 J\rfloor$）。

5. 进一步的显式展开（按 1 位位置计）

为便于实现与校验，我们把 (9) 反复展开。设 $$ J=\sum_{t=0}^k 2^{p_t},\qquad p_k>p_{k-1}>\cdots>p_0\ge 0 $$ 是 $J$ 的 1 位位置（从低位起 0 下标）。不停对“去掉最高位后的尾部”应用 (9)，可得

$$ \boxed{S(J)=\sum_{t=0}^{k} 2^{t}\cdot 4^{p_{k-t}}}. \tag{11} $$

上式的系数 $2^{t}$ 正好等于“严格高于当前 1 位的 1 的个数”的 $2$ 次方。用同样的剥离思路，把 (10) 也完全写开，可得

$$ \boxed{g(J)=4^{p_k}+2\sum_{t=0}^{k-1} 2^{t}\cdot 4^{p_{k-1-t}}-2^{p_k}\cdot \sum_{t=0}^{k-1} 2^{p_t}}. \tag{12} $$

当然，实际编码并不一定采用 (12) 的一次性展开；直接用 (10)+(9) 的“逐位剥离”写成循环（或递归）即可，时间 $O(\text{位数})$。

6. 与题面操作的对接与实现要点（思路）

• 询问保证 $a_l=1$。因此 $\mathrm{val}(l,r)=J$ 的最高位 总是 $2^{k}$（其中 $k=r-l$），即 $$ J=2^k + r,\quad r=\text{把 } a_{l+1}\ldots a_{r} \text{ 看成二进制数（低位在右）}. $$ 于是 $$ g(J)=2S(r)+4^k-2^k r \pmod{10^9+7}. $$ 只需能得到：

  1. 区间长度 $k+1$（显然）；
  2. 区间 $(l+1,\ldots,r)$ 的二进制值 $r$（模 $M$ 即可）；
  3. $S(r)$（模 $M$）。

• 区间翻转 $a_i\leftarrow 1-a_i$ 是典型的“按位取反”的区间操作。可以用懒标记线段树或块状维护两种信息：

  • 数值：$r = \sum b_t 2^{t}$；
  • “$S(\cdot)$”：根据 (9) 的位剥离递推，把一个节点的区间视为“最高位 + 尾部”，即可在合并时得到该区间对应数的 $S$ 值。 若实现上把一个区间拆成“左半（高位段）+右半（低位段）”，则该区间对应的数 $X$ 与 $S(X)$ 可按 (9)(10) 的思想自底向上合并。
  • 懒翻转对这两类量的影响都可在节点内显式推导（对数值是 $r\mapsto (2^{\text{len}}-1)-r$；对 $S$ 可用等价的“位剥离”视角在节点尺度上写出封闭式变换），这里从略。

• 预处理 $\{2^t,4^t\}$ 的幂表即可在模 $10^9+7$ 下常数时间取用。

以上实现细节超出本文数学主线；本题的关键在于把 $f(i,j)$ 化为“子掩码下取下界”的 $s_j(t)$，再通过最高位分治得到 (9)(10)。

7. 小例检验

以样例第一问为例：$\mathrm{val}(1,2)=3$。写成 $J=2^1+r$ 得 $r=1$。

• $S(1)=\sum_{t=1}^{1}s_1(t)=s_1(1)=1$；
• $g(3)=2S(1)+4^1-2^1\cdot 1=2\cdot 1+4-2=4$。吻合样例。

（顺带一提：样例输出展示里第二行把两个答案写在一行了，按照“每个询问一行”的常规应为三行输出。）

8. 结论与复杂度

• 数学结论：对任意 $J=2^k+r,(0\le r<2^k)$，有 $$ \boxed{g(J)=2S(r)+4^k-2^k r,\qquad S(2^k+r)=2S(r)+4^k,~S(0)=0}. $$
• 计算 $g(J)$ 只需沿 $r$ 的二进制位做 $O(\log J)$ 次“去最高位”操作；结合数据结构维护区间的数值与“去最高位递推”，总询问复杂度可达 $O(\log n)$（或块状做 $O(\sqrt n)$），满足约束。

T1

给定 $N$ 条水平线段（“防壁”）和 $M$ 次竖直射线（“镭射”）的位置：

• 第 $i$ 条防壁位于高度（行）$y=i$，初始覆盖横坐标区间 $[A_i,B_i]$。其长度固定为 $B_i-A_i+1$，只能沿水平方向移动。
• 第 $j$ 次镭射在横坐标 $x=P_j$ 处从上到下发射。

要求：在每次镭射发射时，镭射都要穿过每一条防壁。等价地说，在第 $j$ 次发射时，每条防壁的当前覆盖区间都必须包含 $P_j$。

允许的操作：在开始前以及任意两次发射之间，你可以把每条防壁在水平方向上移动若干格；每向左或向右移动 $1$ 格计为 $1$ 次移动。

目标：对每条防壁分别计算为了满足上述要求所需的最少移动次数之和（从初始位置出发、跨越全部 $M$ 次发射的累计移动量）。

• $1\le N,M\le 2\times10^5$

• $0\le A_i\le B_i\le 10^9$

• $0\le P_j\le 10^9$​

3s, 256MiB

T2

给定长度为 $N$ 的序列 $S=(S_1,S_2,\dots,S_N)$，每个元素满足 $1\le S_i\le C$。允许进行一次如下操作：

• 选择一个子串区间 $(i,j)$（$1\le i\le j\le N$），将 $S_i,S_{i+1},\dots,S_j$ 按升序排序后替换原位置，得到新序列 $S'$。

在得到的 $S'$ 中，计算其最长回文子串（连续）的长度。你的任务是：在所有可能的选择 $(i,j)$ 中，最大化该最长回文子串的长度，并输出该最大值。

$1\le N,C\le 3000$，$1\le S_i\le C$​。

4s, 256MiB

T3

给定 $N$ 个区间事件与一扇门的开关规则，时间轴为 $[0,M]$。在时刻 $0$ 与时刻 $M$，所有人都在室内。

• 第 $i$ 个人在时刻 $S_i$ 离开，在时刻 $T_i$ 回来，满足 $0<S_i<T_i<M$。

• 任意两次事件不同步：对所有 $i\neq j$，有 $S_i\ne S_j,\ S_i\ne T_j,\ T_i\ne T_j$。

• 门在时刻 $0$ 处于关闭状态。

• 规则：

  • 在室内可以自由开关门；
  • 在室外只有持钥匙者才能开关门；
  • 进入公司的人，或“持钥匙离开”的人，可以选择是否把门关上；
  • “无钥匙离开”的人无法把门锁上（离开时不能关门）；
  • 第 $i$ 个人能在 $T_i$ 进入，当且仅当 $T_i$ 时刻门是开的，或该人拥有钥匙。

现有 $K$ 把钥匙，必须事先分配给 $K$ 个不同的人。目标是在确保每个人都能在各自的 $T_i$ 成功进入的前提下，使 $[0,M]$ 期间门保持“关闭”的总时长最大。输出这一最大时长。

$1\le N\le 2000,\ 1\le M\le 10^9,\ 1\le K<N$

1s, 256MiB

T1

JOI 公司是一家以“没啥用发明”而闻名的公司。最近，JOI 公司开发了一款名为“没啥用编辑器”的编辑器。

在这个编辑器中，可以执行如下几种操作来输入某个字符串，设 $X$ 为屏幕上的字符串，$Y$ 为剪切板中的字符串，初始均为空串：

• 操作 A：输入字符 $c$，即将 $X$ 更新为 $X+c$。
• 操作 B：选择所有字符并剪切，即将 $Y$ 更新为 $X$，并将 $X$ 置为空串。
• 操作 C：将剪切板中的字符串粘贴到当前字符串末尾，即将 $X$ 更新为 $X+Y$。

对于字符串或字符 $x,y$，$x+y$ 表示将 $x$ 和 $y$ 顺次拼接得到的结果。使用一次操作 A,B,C 分别要花费 $A,B,C$ 单位时间。

你安装了“没啥用编辑器”，并想要尽可能快地输入一个长度为 $N$ 的字符串 $S$。

你需要计算出最少需要花费多少时间。

【数据范围】

对于所有数据，满足：

• $1\leq N\leq 2500$
• $S$ 是一个长度为 $N$ 的小写字母串。
• $1\leq A,B,C\leq 10^9$

3s, 2GiB

T2

D-taro 会给 Anna 一个整数，目标就是让 Anna 将这个整数发送给 Bruno。

游戏开始时，Anna 声明了一个在 $1$ 到 $2000$ 之间的整数 $m$，接下来他们玩 $Q$ 轮游戏。第 $i$ 轮游戏的过程如下：

1. D-taro 向 Anna 给出一个整数 $A_i$。

2. Anna 向通信设备输入两个数组 $s_i,t_i$，数组的每个元素 $s_i,t_i$ 应当是 $0$ 或 $1$，并且两者的长度相同且均为某个 $1$ 到 $m$ 之间的整数。

3. 令 $u_i$ 为 $s_i$ 和 $t_i$ 经过乱序归并得到的结果，通信设备会向 Bruno 发送 $u_i$。

4. Bruno 告诉 D-taro 一个整数，如果这个整数和 $A_i$ 相同，Anna 和 Bruno 在这轮获胜。

以下是乱序归并的定义：

我们称数组 $Z$ 是数组 $X$ 和数组 $Y$ 经过乱序归并得到的结果当且仅当：存在一种划分方式，将 $Z$ 中的元素划成两个集合，满足：

• 第一个集合中的元素按在 $Z$ 中的位置顺次连接得到的数组是 $X$。
• 第二个集合中的元素按在 $Z$ 中的位置顺次连接得到的数组是 $Y$。

例如：数组 $[\underline{1},\underline{1},1,0,0,\underline{0}]$ 可以由数组 $[1,1,0]$ 和数组 $[1,0,0]$ 乱序归并得到。

请你实现 Anna 和 Bruno 的策略。

数据范围与评分方式

• $1\leq Q\leq 1000$
• $1\leq A_i\leq 10^{18}$

Subtasks

• $\text{(5 points) } A_i\leq 2000$
• $\text{(5 points) } A_i\leq 4\times 10^6$
• $\text{(3 points) } A_i\leq 10^7$
• $\text{(12 points) } A_i\leq 10^8$
• $\text{(15 points) } A_i\leq 10^{11}$
• $\text{(60 points)}$ 无特殊限制，评分方式如下：

这个子任务的得分是所有测试点得分的最小值。

对于某个测试点，他的得分由 $m$ 决定，如下表：

T3

JOI 君是一位专业的团子师傅。在 JOI 君的店里，团子的颜色很有讲究。一共有 $N$ 种颜色，编号为 $1,2,\dots,N$。

一流团子串是 JOI 君的店里的招牌食品。制作一个一流团子串，需要将 $N$ 个颜色不同的团子串在一根竹签上。

对于每一种颜色，JOI 君都制作了 $M$ 个这种颜色的团子。因此，JOI 君总共有了 $NM$ 个团子。这些团子被编号为 $1,2,\dots,NM$。使用这些团子和 $M$ 根竹签，JOI 君希望串出 $M$ 个一流团子串。

为了避免在颜色上犯错误，JOI 君将会启用他的团子检测器。如果 JOI 君输入一些团子的编号，团子检测器会返回使用这些团子能制作的一流团子串的个数的最大值。当然，前提是充分使用竹签。

JOI 君希望能通过使用若干次团子检测器将 $NM$ 个团子分为 $M$ 组。其中，每一组包含 $N$ 个团子，且每种颜色的团子恰有一个。

JOI 君想在使用不超过 $50,000$ 次团子检测器的前提下完成这件事。

请写一个程序，对于给定的团子的信息，实现 JOI 君使用不超过 $50,000$ 次团子检测器来完成任务的策略。

【数据范围】

对于所有测试数据，满足：

• $1 \le C_i \le N$ $(1 \le i \le NM)$。
• 对于每个 $j$ $(1 \le j \le N)$，恰有 $M$ 个 $i$ $(1 \le i \le NM)$ 满足 $C_i = j$。
• $N,M$ 是正整数。
• $C_i$ $(1 \le i \le NM)$ 是一个 $[1,N]$ 内的整数。