QOJ1215. Walls 题解

首先显然贪心地移动区间（即每次移动步数最小）是不劣的，直接模拟可以做到 $O(nm)$

第 $i$ 次攻击记为 $a_i$，把一个防壁叫做一个区间 $[l, r]$。

我们先只解决一个区间的答案。

先抛去麻烦的边界情况，即我们默认询问的区间的左端点与第一次攻击的位置相同。

考虑直接做没有什么好的思路，考虑这类题常见的解题思路——优化 $a$ 数组的弱相关元素。但是 $a$ 数组与询问区间的长度息息相关，我们不妨暂时把询问区间的长度看成极小。

略微思考一下发现，若对于满足 $\forall i\in [2, n-1], a_{i-1} < a_i < a_{i+1}$ 条件的攻击 $i$，从 $a_{i-1}$ 移动到 $a_{i+1}$ 时一定会经过 $a_i$——因为区间的移动时连续的。同理，对于 $\forall i\in [2, n-1], a_{i-1} > a_i > a_{i+1}$ 的攻击也可以忽略不计。

那么在删去满足上面条件的元素后，显然剩下的 $a$ 数组形如 $a_1 > a_2 < a_3 > a_4 \ldots$ 或者 $a_1 < a_2 > a_3 < a_4 \ldots$。

发现如果 $|a_i - a_{i+1}|<r-l$ 的话是难做的，为了解决这种情况 我们不妨找出的更特殊一点的 $i$：点 $i$ 满足 $\forall j\in [1, n-1], |a_i - a_{i+1}| \le |a_j - a_{j+1}|$，也就是和下一个相邻的 $a_i$ 差最小的位置。我们考虑普遍的情况并画出其中一种情况的图：（另一种类似）

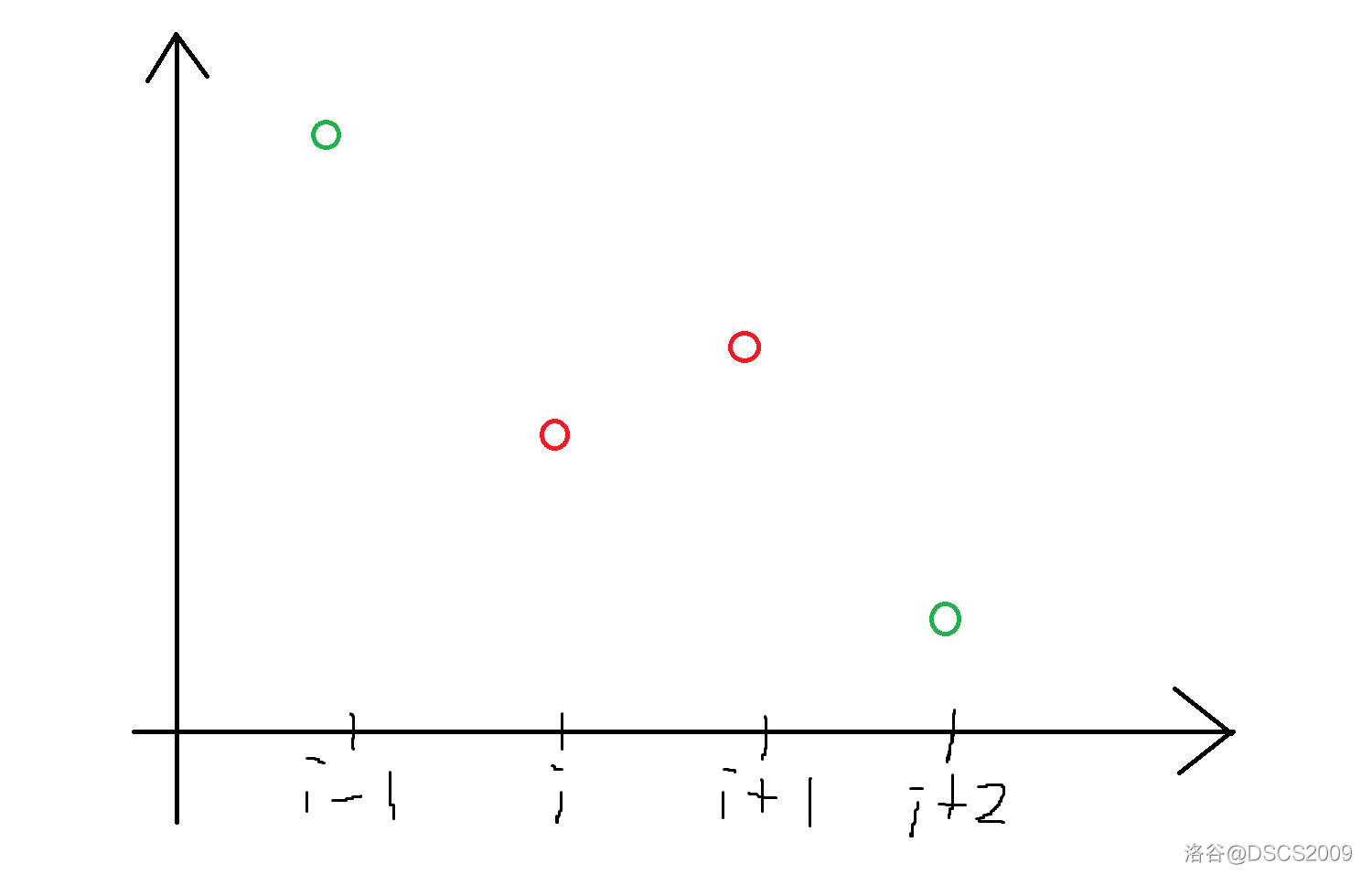
可以得到 $a$ 的一些偏序关系：$a_{i-1} \ge a_{i+1} \ge a_i \ge a_{i+2}$。

那么模仿上面的证明过程，若区间能到达 $a_{i-1}$，那么在区间前往覆盖 $a_{i+2}$ 的过程中，一定有时刻满足区间左端点经过了 $a_i$，而若区间左端点覆盖了 $a_i$，由 $|a_i - a_{i+1}| \le d$，可知区间一定覆盖了 $a_{i+1}$。因此我们可以直接删掉 $a_i$ 和 $a_{i+1}$。

考虑一下边界情况（情况同样参照上面那副图，另一种情况同理）：

若既不存在 $a_{i-1}$ 也不存在 $a_{i+2}$，那么我们不删除 $a_i$ 和 $a_{i+1}$，此时只剩两个 $a_i$，可以暴力模拟。

若只存在 $a_{i-1}$，则删除 $a_{i+1}$，因为到达 $a_i$ 与到达 $a_{i+1}$ 等价，且从 $a_{i-1}$ 到 $a_i$ 时左端点必须经过 $a_i$。

若只存在 $a_{i+2}$，则删除 $a_i$，因为从 $a_{i+1}$ 到达 $a_{i+2}$ 时左端点一定经过 $a_i$。不能删除 $a_{i+1}$ 的原因是从 $a_i$ 到 $a_{i+2}$ 不一定满足左端点一定经过 $a_i$。

现在问题变成了 $\forall i,|a_i - a_{i+1}|\geq r-l$，那么答案就是先将区间移到 $a_1$，然后答案加上 $\sum_i[|a_i - a_{i+1}|-(r-l)]$​。

我们对于一个区间做到了除了删 $a_i$ 部分的 $O(1)$。

显然长度大的区间的删除点集合包含长度小的删除点集合，我们可以把询问按照长度排序然后每次删点继承上次删点即可做到均摊 $O(\log n)$。

时间复杂度 $O((N+M)\log M)$。

QOJ1210. AAQQZ 题解

选择某个排序区间后，我们围绕回文中心处理这部分。

我们先 $O(n^2)$ 预处理出 f[i][j]，表示以 $i,j$ 为左、右端点，在原串上再向外扩展匹配能匹配多少位置。形式化地说，是最大的 $k$ 满足 $\forall x\in[0,k-1], S_{i-x}=S_{j+x}$。

此时对于一个固定的回文中心分为 $6$ 种情况。

1. 回文区间和排序区间不交

2. 回文中心被包含在排序区间，且不在排序区间排序后的值最小/大段（也是排序区间中最左/右的相同值构成的连续段）

3. 回文中心被包含在排序区间，且在排序区间排序后的值最小/大段，且回文区间包含排序区间

4. 回文中心被包含在排序区间，且在排序区间排序后的值最小/大段，且回文区间不包含排序区间

5. 回文中心不被包含在排序区间，且回文区间包含排序区间

6. 回文中心不被包含在排序区间，且回文区间不包含排序区间

情况 $1$ 时，答案就是在不排序下的最长回文子串。

对于情况 $2$，发现答案就是该回文中心在同值连续段进行扩展，能扩展到的最大长度。这种情况可以通过将整个字符串排序，那么此时最长同值连续段的长度就是所有回文中心和排序方案在满足情况 $2$ 下的最长回文子串。

对于情况 $3/4$，发现回文中心不在排序区间排序后的值最小/大段的中点是严格劣的。

不妨令回文中心在排序区间最小段，排序区间其余部分在回文中心右部。

先解决情况 $4$，先把中间的排序区间排序后的值最小段扔掉，发现对于已经排序完的右部分，能够匹配的合法的左部分只能是一个单调不增的连续段。先将这个连续段 $O(n)$ 暴力算出来，然后逐渐扩展右部。我们称左部为需求 Lcnt，右部为供给 Rcnt，Lcnt[i] 代表左部有几个 $i$，Rcnt 同理。设当前右部扩展到了 k，那么首先需要匹配右部值域上的前缀区间可用当且仅当满足 $\forall i,\text{Lcnt}[i]=\text{Rcnt}[i]$。发现一旦 $\exist i, Lcnt[i]<Rcnt[i]$，那么后面无论如何扩展，$>i$ 的前缀部分都没救了，此时应当对值域进行截断操作。可以双指针维护右部值域上的前缀区间，做到 $O(n)$。

再解决情况 $3$，发现这种情况的回文区间就是 在 【不存在没救的部分的】情况 $4$ 的回文区间 $[L,R]$ 接上 【f[L-1][R+1] 所代表的回文部分】 得到的回文区间。（如果存在没救的部分，那么 【f[L-1][R+1] 所代表的回文部分】 就因为中间的 【没救部分所带来的未匹配空位】 而无法接上）

对于情况 $5/6$，这种情况就是先将回文中心的 【f[i][i] 或 f[i][i+1]（取决于回文区间长度的奇偶性）所代表的回文部分】 扔掉，再做一遍情况 $3/4$ 在 “先把中间的排序区间排序后的值最小段扔掉” 后的步骤。

枚举完回文中心后，所有情况的分讨都是 $O(n)$ 的。

总时间复杂度 $O(n^2)$。

QOJ1209. Keys 题解

我们称一个员工的进出为一个事件。

我们不妨将所有事件按照事件发生的时间点排序，我们假设 $i$ 为触发一个事件的员工，$j$ 为下一个时间点触发事件的员工，考虑每种情况对答案（也就是大门锁的时间）什么时候有贡献，我们可以分成 $4$ 类来讨论：

• $i$ 进来，$j$ 出去，那么 $i$ 绝对会关门，我们将区间贡献直接加到答案上。
• $i$ 进来，$j$ 进来，$i$ 关门时当且仅当 $j$ 有钥匙，我们将贡献加到 $j$ 员工上。
• $i$ 出去，$j$ 出去，$i$ 关门时当且仅当 $i$ 有钥匙，我们将贡献加到 $i$ 员工上。
• $i$ 出去，$j$ 进来，这段区间有贡献当且仅当 $i, j$ 都有钥匙，如果 $i, j$ 是同一个人，将贡献直接加到 $i$ 上，否则将 $i, j$ 连一条有向边，将贡献加到 $i \to j$ 的边上面。

这样我们就转换成了一个图上问题，不难发现这个图是由若干条链组成的（因为每个员工只有两种状态），我们不妨将这些链组成一个大链，对这个链式序列 DP 即可。

记 $\text{v1}_i$ 表示 $i$ 点权，$\text{v2}_i$ 表示 $i$ 到连接到的那个点的边权。

我们设 $f_{i,j,0/1}$ 表示当前链的前面 $i$ 个人，共有 $j$ 把钥匙，第 $i$ 个人是否有钥匙的最大贡献。

若第 $i$ 个人没有钥匙，那么有 $f_{i,j,0} = \max\{f_{i,j,0}, f_{i-1,j,1}, f_{i-1,j,0}\}$。

若第 $i$ 个人有钥匙，那么有 $f_{i,j+1,1} = \max\{f_{i,j+1,1}, f_{i-1,j,0} + \text{v1}_i, f_{i-1,j,1} + \text{v1}_i + \text{v2}_i\}$。

（这个边两端点都有 $1$，因此两点之间有边，所以要加上边权）

$f$ 第一维显然能被滚动数组优化掉，时间复杂度 $O(n^2)$，空间复杂度 $O(n)$。